Link:https://marypatcampbell.substack.com/p/covid-data-follies-vaccination-rates
Video:
Graphic:
Excerpt:
On Monday, December 6, 2021, I gave a talk with the title “COVID Data Follies: Vaccination Rates, Relative Risk, and Simpson’s Paradox”, to the Actuarial Science program at Illinois State University (thanks for the t-shirt, y’all!):
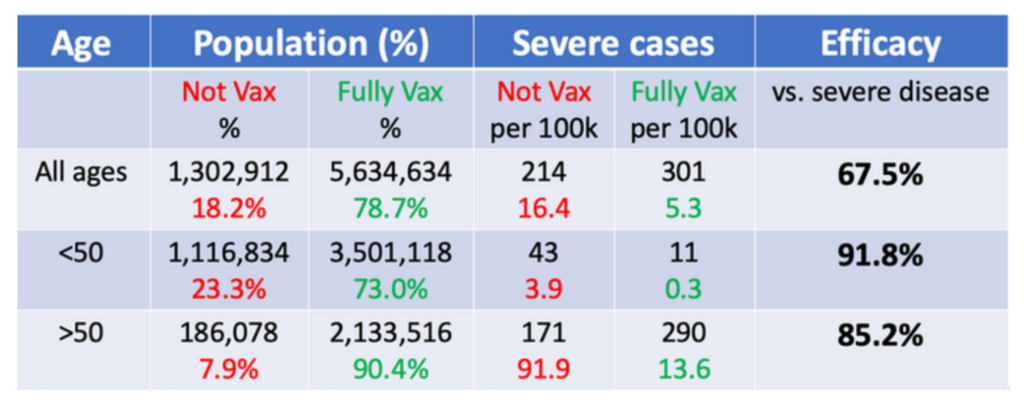
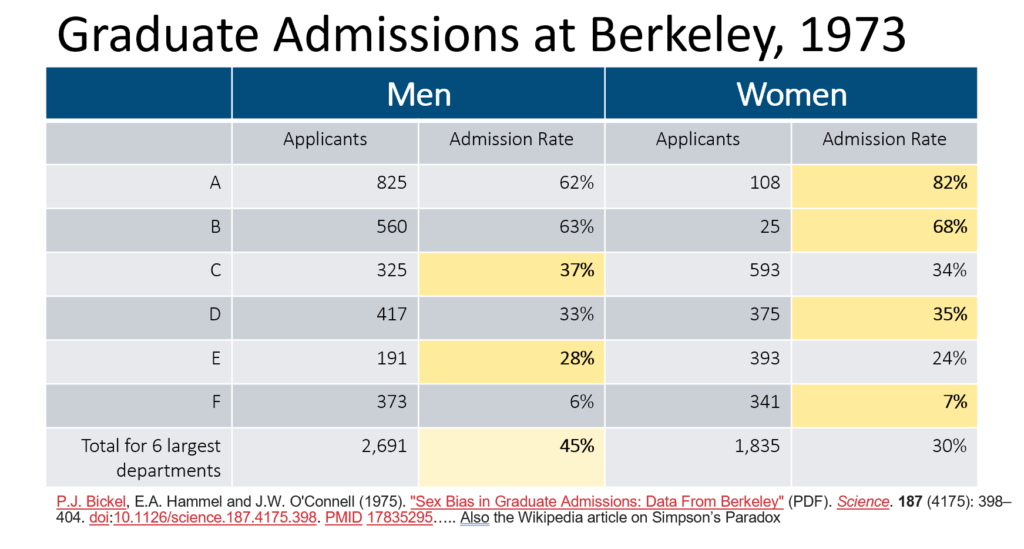
You may have heard statistics in the news that most of the people testing positive for COVID, currently, in a particular location, or most of the people hospitalized for COVID, or even most of the people dying of COVID were vaccinated! How can that be? Does that prove that the vaccines are ineffective? Using real-world data, the speaker, Mary Pat Campbell, will show how these statistics can both be true and misleading. Simpson’s Paradox is involved, which has to do with comparing differences between subgroups with very different sizes and average results. Simpson’s Paradox actually appears quite often in the insurance world.
I will embed a recording of the event, copies of the slides, the spreadsheets, and the links from the talk.
Author(s): Mary Pat Campbell
Publication Date: 8 Dec 2021
Publication Site: STUMP at substack